Andree Heseler
Challenger vs. Champion: Wie KI-Modelle klassische Verfahren herausfordern
3 Implementierung des Validierungsprozesses
3.1 Erweiterter Validierungsprozess
Die Validierung von Risikomodellen gehört zu den zentralen Aufgaben des Risikomanagements in Banken. Während klassische Validierungsverfahren – insbesondere bei linearen Modellen wie der logistischen Regression – weitgehend standardisiert und etabliert sind, stellt die zunehmende Integration komplexerer Modelle, etwa auf Basis von KI, neue Anforderungen an Aufbau, Ablauf und Tiefe des Validierungsprozesses
Vor diesem Hintergrund schlagen wir einen erweiterten Validierungsprozess vor, der sich an den klassischen Prüfstrukturen orientiert, diese jedoch um wesentliche Komponenten ergänzt. Der Prozess umfasst drei zentrale Erweiterungen:
Einbindung von Challenger-Modellen mit KI‑Methodik:
Zur Prüfung der Leistungsfähigkeit bestehender Produktivmodelle werden alternative Modellansätze auf Basis moderner Machine-Learning-Methoden, etwa XGBoost, herangezogen. Ziel ist es, durch systematischen Vergleich Hinweise auf potenzielle Verbesserungen der Trennschärfe, Kalibrierung oder Robustheit zu erhalten. Darüber hinaus bietet der Einsatz nicht linearer Modelle die Möglichkeit, versteckte Interaktionen zwischen Risikofaktoren zu identifizieren.
Multi‑Model‑Management:
In komplexeren Modelllandschaften ist es nicht mehr ausreichend, einzelne Modelle isoliert zu bewerten. Stattdessen bedarf es eines strukturierten Frameworks zur simultanen Bewertung mehrerer Modelle, Modellvarianten und Datenschnitte. Dieses Framework erlaubt:
- die Orchestrierung verschiedener Modellläufe,
- die Aggregation und Speicherung zentraler Kennzahlen (z. B. AUC/Gini, Brier-Score) in mehrdimensionalen Datenstrukturen (z. B. Data Cubes)
- und die Durchführung standardisierter Vergleichs- und Signifikanztests zur objektiven Entscheidungsunterstützung.
Automatisierung und Modularisierung der Analyseprozesse:
Die zunehmende Komplexität der Modelllandschaft und die steigenden regulatorischen Anforderungen verlangen nach einem hohen Maß an Prozessautomatisierung. Ziel ist es, Validierungsschritte nicht nur reproduzierbar, sondern auch skalierbar und transparent zu gestalten. Die modulare Architektur der Analysekomponenten – insbesondere im Bereich der Kreuzvalidierung, Modellvergleiche und Erklärbarkeitsanalysen – erlaubt die einfache Erweiterung auf zusätzliche Modelle oder Datenquellen.
Die Kombination dieser drei Erweiterungen bildet das Fundament eines modernen, validierungsfähigen Risikomodell‑Frameworks im Zeitalter der datengetriebenen Entscheidungsfindung. Durch die Anwendung dieses Frameworks im Rahmen der nachfolgenden Fallstudie wird exemplarisch gezeigt, wie sich das vorgeschlagene Validierungskonzept in der praktischen Modellbewertung einsetzen lässt – mit Fokus auf Erklärbarkeit, Modellvergleich und quantitativer Aussagekraft.
3.2 Aufteilung in Trainings- und Testdaten (Kreuzvalidierung)
Ein zentrales Element jeder belastbaren Modellvalidierung ist die konsequente Trennung von Trainings- und Testdaten. Nur durch eine klare Abgrenzung zwischen Modellkalibrierung und Evaluation lassen sich Aussagen zur generalisierten Leistungsfähigkeit eines Modells treffen. Dies gilt in besonderem Maße für moderne KI‑Modelle, deren Flexibilität gleichzeitig eine erhöhte Gefahr des Overfittings mit sich bringt.
In der Praxis hat sich für solche Validierungsvorhaben die k-Fold‑Kreuzvalidierung als Standardverfahren etabliert. Dabei wird der vollständige Datensatz in k gleich große Teilmengen (sog. Folds) unterteilt. In jedem der k‑Validierungsläufe werden k‑1‑Folds zum Modelltraining verwendet, während der verbleibende Fold für die Modellprüfung (Out-of-Sample-Evaluation) dient. Durch zyklisches Rotieren der Test-Folds wird sichergestellt, dass jede Beobachtung genau einmal im Testset enthalten ist.
Abbildung 1: k-Fold-Kreuzvalidierung (k = 5)
3.3 Multi‑Model‑Management
In modernen Modell‑Architekturen gewinnt die gleichzeitige Bewertung mehrerer Modelle zunehmend an Bedeutung. Gründe hierfür sind unter anderem regulatorische Anforderungen an die regelmäßige Modellüberprüfung und die Einschätzung des Modellrisikos, technologische Fortschritte im Bereich Machine Learning, aber auch die strategische Zielsetzung, stets die leistungsfähigsten Modelle im Einsatz zu haben. Den Ansatz, mehrere Modellalternativen gleichzeitig zu entwickeln, zu validieren und vergleichend gegenüberzustellen, bezeichnen wir als Multi‑Model‑Management.
Das hier vorgestellte Multi‑Model‑Framework erweitert klassische Validierungslogiken um einen strukturierten, systematischen Vergleich unterschiedlicher Modellvarianten entlang definierter Bewertungskriterien. Es adressiert insbesondere folgende Herausforderungen:
Orchestrierung heterogener Modelllandschaften:
In einer produktiven Umgebung existieren typischerweise mehrere Modellvarianten mit unterschiedlichen Methoden (z. B. Logit, XGBoost, neuronale Netze), Parametrisierungen oder Trainingsdatenschnitten. Diese Vielfalt erfordert eine koordinierte Durchführung und Zusammenführung der Validierungsläufe.
Standardisierte Metrikerhebung und Persistenz:
Für jede Modellinstanz werden zentrale Modellgütekennzahlen – insbesondere AUC/Gini-Koeffizient und Brier-Score – erhoben, standardisiert und in mehrdimensionalen Analyse-Cubes gespeichert. Diese Datenstruktur erlaubt schnelle, konsistente Auswertungen und ermöglicht auch retrospektive Analysen über verschiedene Zeitpunkte oder Modellgenerationen hinweg.
Vergleichbarkeit und Entscheidungsunterstützung:
Basierend auf den validierten Metriken wird eine Modellrangfolge ermittelt. Hierzu kommen unter anderem Rangordnungsverfahren (Ranking der Modelle je Kreuzvalidierungslauf) sowie statistische Signifikanztests oder auch Bayes’sche Statistiktests (z. B. Friedman‑Test, Rom-Prozedur, ROPE-Ansatz) zum Einsatz.10 Diese erlauben eine fundierte, objektivierbare Entscheidung über die relative Leistungsfähigkeit der Modelle.
Modularität und Erweiterbarkeit:
Das objektorientierte Framework ist so konzipiert, dass neue Modelle, weitere Gütemaße oder zusätzliche Validierungstechniken (z. B. Explainable AI, Stressszenarien) mit minimalem Integrationsaufwand eingebunden werden können. Dies gewährleistet eine nachhaltige Einsetzbarkeit auch in sich dynamisch entwickelnden Modellumgebungen.
In Summe bildet das Multi-Model-Management den methodischen Kern einer modernen, transparenten und zukunftsfähigen Modell-Governance. Es befähigt Institute dazu, sowohl regulatorischen Anforderungen zu genügen als auch technologische Innovationen gezielt in ihre Entscheidungsprozesse zu integrieren.
Im folgenden Kapitel erfolgt auf dieser Grundlage die exemplarische Anwendung auf zwei konkrete Modelle – eine logistische Regression und ein XGBoost-Modell – unter Verwendung eines realitätsnahen Kreditportfolios.
4 Modellergebnisse im Vergleich
Nach der methodischen Herleitung und Definition des Validierungsrahmens folgt nun die empirische Anwendung. Ziel ist es, anhand eines realitätsnahen Datensatzes die Leistungsfähigkeit zweier Modellansätze – einer klassischen logistischen Regression (Modell A) und eines modernen XGBoost-Modells (Modell B) – vergleichend zu analysieren. Dabei steht nicht nur die reine Vorhersagegüte im Vordergrund, sondern auch die Frage, inwiefern komplexere Modelle zusätzliche Informationen liefern und wie diese erklärbar gemacht werden können.
Tabelle 1: Beschreibung der Eingangsmerkmale
Die Zielvariable BAD kodiert den Ausfallstatus binär (1 = ausgefallen, 0 = nicht ausgefallen) und stellt damit die abhängige Variable für die Modellschätzung dar.
Vorverarbeitung und Merkmalsselektion:
- Fehlende Werte wurden durch Mittelwertimputation ersetzt.
- Alle numerischen Merkmale wurden standardnormalisiert (Z-Transformation), um numerische Stabilität bei der Modellschätzung sicherzustellen.
- Die stark korrelierten Merkmale MORTDUE und VALUE wurden auf eines reduziert; kategorische Merkmale wie JOB und REASON wurden zur Komplexitätsreduktion nicht berücksichtigt.
Diese Selektion bildet die Grundlage für die nachfolgende Kalibrierung und Validierung beider Modelle.
4.2 Ergebnisse des Logit-Modells (Modell A)
Das erste Modell basiert auf einer logistischen Regression, einem etablierten Verfahren zur Modellierung binärer Zielgrößen. Ziel ist die Schätzung der bedingten Wahrscheinlichkeit eines Kreditereignisses (Ausfall/Nichtausfall) in Abhängigkeit von den Eingangskriterien.
Das Modell wurde zunächst mit dem vollständigen Datensatz kalibriert (In‑Sample), um eine erste Einschätzung der Modellstruktur und der Koeffizientenstabilität zu erhalten. Die Regressionskoeffizienten bestätigen die statistische Signifikanz nahezu aller Merkmale
(p-Wert ≈ 0,0), mit Ausnahme von YOJ (p-Wert = 0,23).
Signifikanz und Richtung der Effekte
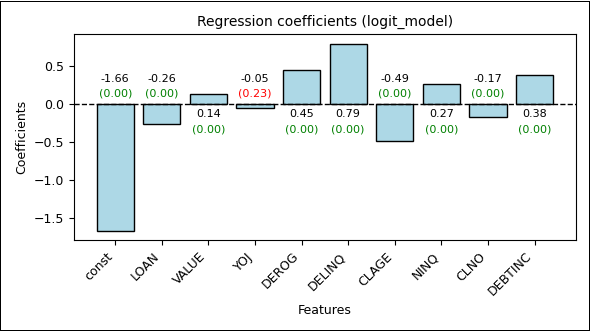
Positiv wirkende Merkmale sind VALUE, DEROG, DELINQ, NINQ, DEBTINC. Negativ wirkende Merkmale sind LOAN, CLAGE, CLNO, YOJ, const. Die Konstante (const) des Modells beträgt -1,66, was einer geschätzten Basis-Ausfallwahrscheinlichkeit von etwa 15,93 % entspricht – in realistischer Nähe zur beobachteten Ausfallrate von 19,95 %.
Abbildung 2: Regressionskoeffizienten des trainierten Logit-Modells (p-Werte in Klammern)
Die zentralen Modellmetriken lauten:
| Kennzahl | Wert | Interpretation |
|---|---|---|
| AUC/Gini | 0,79/0,58 | Solide Trennschärfe, aber deutlich unter dem theoretischen Optimum |
| Brier-Score | 0,12 | Akzeptable Kalibrierung der Wahrscheinlichkeiten |
Tabelle 2: Ergebniskennzahlen des Logit-Modells (In-Sample)
Im Anschluss wurde eine fünffache Kreuzvalidierung durchgeführt. Das Modell wurde dabei fünfmal neu trainiert und auf jeweils disjunkte Testdaten angewandt (Out-of-Sample-Prognose). Die Verteilung der Scores zeigt eine zufriedenstellende Trennung der Klassen, allerdings mit systematischen Schwächen in der Erkennung tatsächlicher Ausfälle:
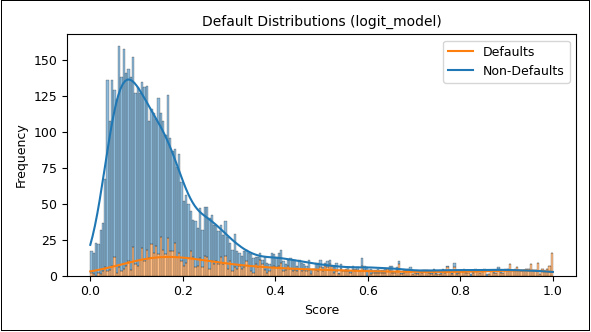
Abbildung 3: Score-Verteilung Logit-Modell (Defaults und Non-Defaults)
Nicht ausgefallene Kredite dominieren den unteren Score-Bereich (niedrige Ausfallwahrscheinlichkeit) – erwartungskonform. Ausgefallene Kredite verteilen sich relativ gleichmäßig über den gesamten Score‑Bereich, jedoch auch mit einem unerwünschten Häufungsschwerpunkt im Bereich (0,1–0,3), was auf eine eingeschränkte Trennschärfe bei risikobehafteten Fällen hindeutet.
Fazit
Das Logit‑Modell bildet eine robuste Basis, weist jedoch Einschränkungen in der Abbildung wahrscheinlich nicht linearer Zusammenhänge auf. Die Identifikation von Defaults ist insbesondere im oberen Score‑Spektrum unzureichend – ein Hinweis auf strukturelle Modellgrenzen.
4.3 Ergebnisse des XGBoost-Modells (Modell B)
Das zweite Modell basiert auf dem XGBoost-Algorithmus, einem gradientenbasierten Ensemble‑Verfahren, das in zahlreichen Benchmark-Studien eine hohe Vorhersagequalität zeigt. Das Modell wurde als binärer Klassifikator konfiguriert mit logistischer Verlustfunktion und logarithmischem Loss als Bewertungsmetrik.
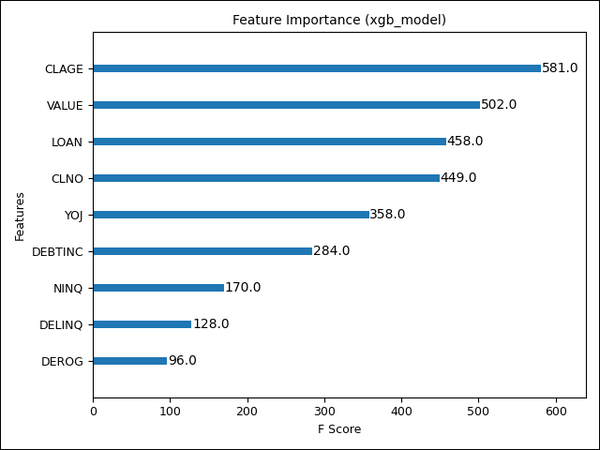
Im Gegensatz zur logistischen Regression basiert XGBoost nicht auf Regressionskoeffizienten, sondern auf der sequenziellen Optimierung von Entscheidungsbäumen. Eine erste Einschätzung der Feature-Wichtigkeit erfolgt daher über die Häufigkeit der Merkmalsnutzung (Feature Importance).
Abbildung 4: Importance-Liste der Merkmale im XGBoost-Modell
| Kennzahl | Wert | Interpretation |
|---|---|---|
| AUC/Gini | 0,99/0,99 | Nahezu perfekte Trennschärfe |
| Brier-Score | 0,007 | Extrem präzise Kalibrierung |
Tabelle 3: Ergebniskennzahlen XGBoost (In-Sample)
Die anschließende fünffache Kreuzvalidierung bestätigt die außerordentliche Modellgüte auch in der Out‑of‑Sample‑Bewertung. Die Verteilung der Scores zeigt eine deutlich klarere Trennung der Ausfallklassen:
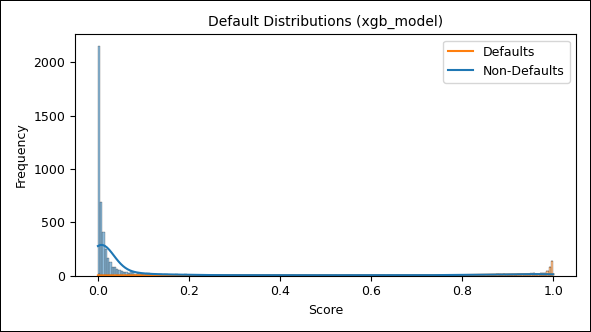
Abbildung 5: Scoring-Verteilung XGBoost (Default vs. Non-Default)
Da die Default-Verteilung in der Abbildung oben aus Skalierungsgründen kaum zu erkennen ist, wird sie in der nächsten Abbildung nochmals separat dargestellt:
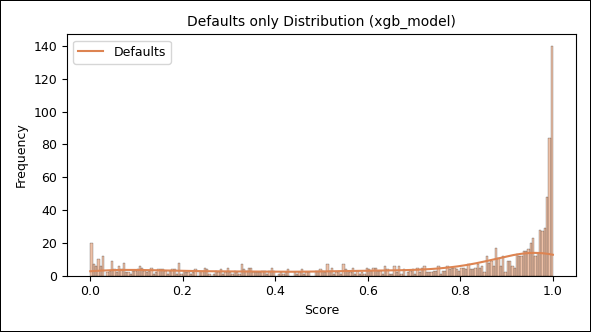
Abbildung 6: Scoring-Verteilung XGBoost (nur Default)
Nicht ausgefallene Kredite weisen eine starke Konzentration im Bereich niedriger Scores (nahe null) auf. Ausgefallene Kredite häufen sich erwartungskonform im Bereich höherer Scores (ab ca. 0,8) – mit deutlich geringerer Streuung im mittleren Segment. Nichtsdestoweniger beobachten wir auch hier ein scheinbar gleichverteiltes Grundrauschen von Ausfällen über den gesamten Score‑Bereich, wenn auch deutlich geringer als beim Logit‑Ansatz. Wünschenswert wäre ein monotones Ansteigen der Ausfälle. Ein möglicher Hinweis auf Modelllücken!
Fazit:
Das XGBoost‑Modell zeigt sowohl hinsichtlich Trennschärfe als auch Kalibrierung eine signifikant überlegene Leistungsfähigkeit gegenüber dem Logit‑Modell. Dennoch bleibt eine kritische Auseinandersetzung mit möglichen Overfitting-Tendenzen geboten, insbesondere vor dem Hintergrund hoher Modellkomplexität und regulatorischer Erklärbarkeitsanforderungen.
4.4 Vergleich der Model Scores mittels Streudiagramm
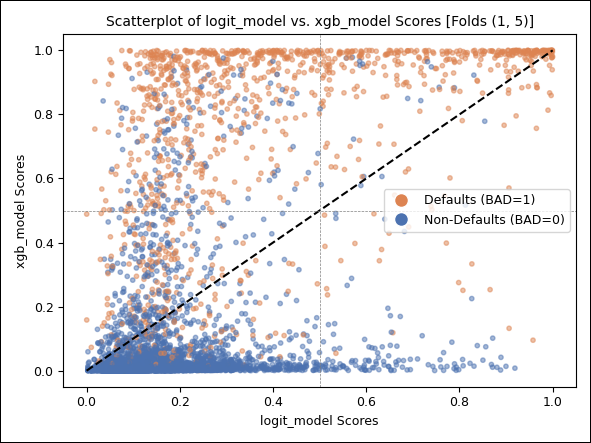
Ein zentrales Ziel der Validierung ist nicht nur die isolierte Bewertung einzelner Modelle, sondern insbesondere deren direkter Vergleich im Verhalten gegenüber identischen Kreditereignissen. Zur Visualisierung der Score‑Differenzen beider Modelle wird ein zweidimensionaler Scatterplot herangezogen, in dem die Score-Werte des Logit‑Modells gegen jene des XGBoost‑Modells aufgetragen werden. Jeder Punkt im Plot repräsentiert ein Kreditereignis, farblich differenziert nach Ausfallstatus.
Abbildung 7: Modellvergleich, Scatterplot
Erste Erkenntnisse
Eine signifikante Anzahl tatsächlicher Ausfälle befindet sich im linken oberen Quadranten – diese Kredite wurden vom Logit‑Modell zu optimistisch, vom XGBoost‑Modell korrekt als kritisch eingeschätzt.
Die Mehrzahl gesunder Kredite konzentriert sich im linken unteren Quadranten – ein Indikator für hohe Übereinstimmung in der Einschätzung geringer Risiken.
Diese Visualisierung liefert wertvolle Hinweise auf die differenzierte Modelllogik der beiden Ansätze und legt den Grundstein für eine quantitative Bewertung der Fehlereinschätzungen, wie sie im folgenden Abschnitt erfolgt.
4.5 Quantifizierung der Modellunterschiede über Fehlerquadrate
Zur objektiven Beurteilung, welches Modell die realisierten Ausfallwahrscheinlichkeiten besser approximiert, greifen wir erneut auf die Ansatzlogik des Brier-Scores zurück. Für jede Beobachtung i wird der quadratische Fehler zwischen der vorhergesagten Wahrscheinlichkeit  und dem tatsächlichen Ausfallstatus
und dem tatsächlichen Ausfallstatus berechnet:
berechnet: 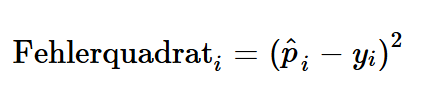
Zur Modellvergleichbarkeit wird die Differenz der Fehlerquadrate zwischen Modell A (Logit) und Modell B (XGBoost) für jede Beobachtung berechnet: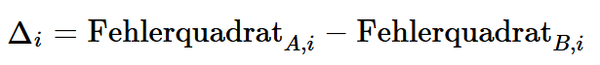
Ein positiver Wert bedeutet, dass Modell B (XGBoost) eine geringere Abweichung vom tatsächlichen Ausfallstatus aufweist – also die bessere Vorhersage liefert.
bedeutet, dass Modell B (XGBoost) eine geringere Abweichung vom tatsächlichen Ausfallstatus aufweist – also die bessere Vorhersage liefert.
Ergebnisse
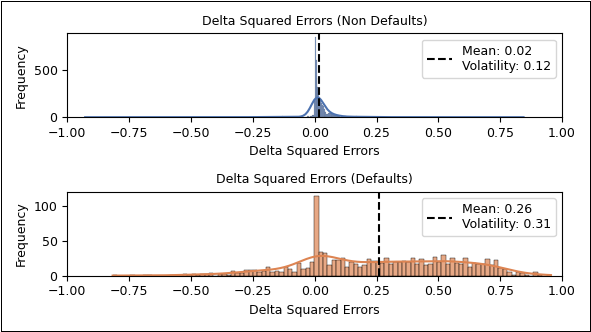
Für nicht ausgefallene Kredite liegen die mittleren Differenzen nahe null (Mittelwert ≈ 0,01), was auf vergleichbare Vorhersagegüte hindeutet.
Für ausgefallene Kredite ergibt sich ein deutlich positiver Mittelwert der Differenzen (≈ 0,24), was die Überlegenheit von XGBoost bei der korrekten Identifikation von Defaults bestätigt.
Eine ergänzende Darstellung in Form von Verteilungsplots visualisiert die Differenzen der Fehlerquadrate getrennt nach Ausfallstatus und macht sichtbar, dass der größte Teil der Modellabweichung durch falsch eingeschätzte Ausfälle im Logit-Modell verursacht wird.
Abbildung 8: Vergleich der Modellgüte anhand der Fehlerquadrat-Abweichung
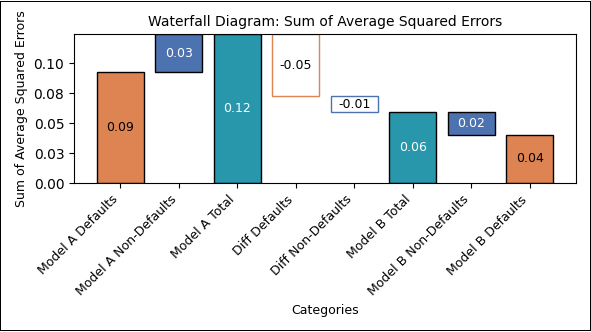
Darauf aufbauend haben wir die aggregierten Modellfehler pro Gruppe (Modell x Ausfallstatus) analysiert und im Kontext des gesamten Brier-Scores interpretiert. Dadurch wird sichtbar, in welchem Maße Ausfälle und Nichtausfälle jeweils zum Gesamtfehler beitragen. So lassen sich Unterschiede in der Modellgüte differenzierter bewerten – insbesondere, ob ein Modell eher im Bereich der „False Negatives“ (nicht erkannte Defaults) oder der „False Positives“ (fälschlich als riskant eingestufte Non-Defaults) Schwächen zeigt.
Die Resultate werden in der folgenden Abbildung als Wasserfalldiagramm zusammengefasst:
Abbildung 9: Modellvergleich Brier-Score-Differenzen
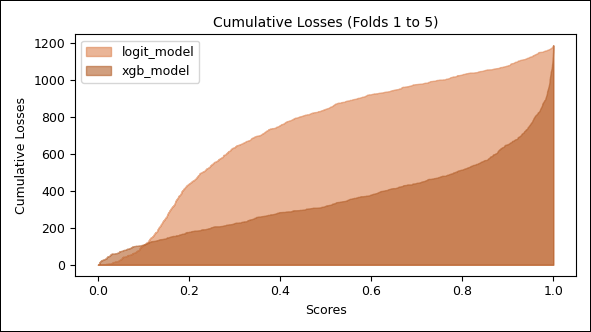
4.6 Vergleich der kumulativen Verlustverteilung
Neben der Bewertung statistischer Gütekriterien ist es aus Sicht des Risikomanagements essenziell, auch die ökonomische Relevanz von Modellunterschieden zu quantifizieren. Während Trennschärfe und Kalibrierung Hinweise auf die technische Leistungsfähigkeit eines Modells geben, stellt sich in der Praxis stets die Frage: Welchen Einfluss hat die Wahl eines bestimmten Modells auf tatsächliche Verluste?
Zur Beantwortung dieser Frage analysieren wir die kumulative Verlustverteilung beider Modelle. Im Zentrum steht dabei die Fragestellung: Wie viele tatsächliche Ausfälle hätte ein Modell übersehen, wenn man die Kreditereignisse mit den höchsten prognostizierten Ausfallwahrscheinlichkeiten abgelehnt hätte?
Methodisches Vorgehen
Die Kreditereignisse werden nach ihrem Score‑Wert (geschätzte Ausfallwahrscheinlichkeit) sortiert – getrennt für jedes Modell. Für einen gegebenen Schwellenwert 𝜏 wird bestimmt, wie viele tatsächliche Ausfälle sich unterhalb dieses Schwellenwerts befinden. Die kumulierten Anteile der erfassten Defaults werden über alle Schwellenwerte hinweg aufgetragen. Das Ergebnis ist eine kumulative Verteilungsfunktion der tatsächlichen Verluste als Funktion der Score‑Schwelle.
Abbildung 10: Modellvergleich, kumulative Verlustverteilung
Ergebnisse der Analyse
Das Logit‑Modell weist bereits bei niedrigen Score-Schwellen (z. B. 0,2) eine signifikante Anzahl von Ausfällen auf – ein Hinweis auf eingeschränkte Trennschärfe.
Das XGBoost‑Modell hingegen verschiebt die Mehrheit der Ausfälle in höhere Score‑Bereiche – ein erwünschtes Verhalten, da es eine effektivere Selektion von Hochrisikofällen erlaubt.
Der Vorsprung von XGBoost in der Identifikation von Defaults ist bis auf einen kleinen Bereich nahe null über alle Score‑Schwellen hinweg konsistent und visuell klar erkennbar.
Praktische Relevanz
Diese Analyse erlaubt nicht nur eine Bewertung der Modellqualität im Sinne klassischer Backtesting-Logiken, sondern bietet auch eine Ableitung von Score‑Schwellen, die zur Steuerung der Kreditvergabe verwendet werden könnten. Modelle mit besserer Verlusttrennung weisen somit nicht nur eine höhere Vorhersagekraft auf, sondern auch einen höheren ökonomischen Nutzen durch gezieltere Risikoallokation.
5 SHAP-Analysen
Mit der wachsenden Komplexität von Scoring-Modellen – insbesondere im Kontext von Machine Learning – rückt die Erklärbarkeit von Modellentscheidungen zunehmend in den Fokus von Risikomanagement und Aufsicht. Der AI Act und diverse Veröffentlichungen der EBA13, aber auch der BaFin14 betonen unmissverständlich: Auch leistungsfähige, nicht lineare Modelle müssen nachvollziehbar und überprüfbar bleiben.
Ein leistungsfähiges Instrument zur Herstellung dieser Transparenz ist das SHAP‑Verfahren (SHapley Additive exPlanations), das auf spieltheoretischen Prinzipien basiert.15 Es erlaubt, für jede einzelne Vorhersage zu bestimmen, welcher Anteil eines Merkmals zum Abweichen der Prognose vom Basiswert beigetragen hat.
5.1 Grundlagen und Darstellung
Formal lässt sich jede Modellvorhersage f(x) durch die SHAP-Dekomposition darstellen als: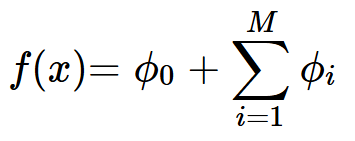
Dabei ist: : der Basiswert (Durchschnitt der Modellvorhersagen),
: der Basiswert (Durchschnitt der Modellvorhersagen), : der SHAP-Wert des Merkmals xi, d. h. dessen individueller Beitrag zur Abweichung vom Mittelwert.
: der SHAP-Wert des Merkmals xi, d. h. dessen individueller Beitrag zur Abweichung vom Mittelwert.
Diese additive Zerlegung ermöglicht sowohl eine globale Analyse der Merkmalsbedeutung als auch eine lokale Erklärung einzelner Modellentscheidungen.
5.2 Vergleich Logit vs. XGBoost anhand individueller Vorhersagen
Die Stärke der SHAP-Analyse zeigt sich insbesondere im Vergleich zweier Modellentscheidungen bei einer identischen Beobachtung. Anhand ausgewählter Fälle lässt sich die Unterschiedlichkeit der internen Modelllogiken präzise aufzeigen.
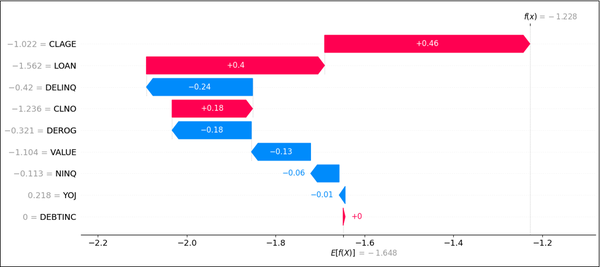
Die folgenden zwei Abbildungen zeigen beispielhaft die SHAP-Werte der beiden Modelle in Form eines Wasserfalldiagramms für einen ausgefallenen Kredit mit den Merkmalen x aus dem oberen linken Quadranten im Scatterplot (Abbildung 7).16
Abbildung 11: SHAP-Wasserfalldiagramm, Logit-Modell
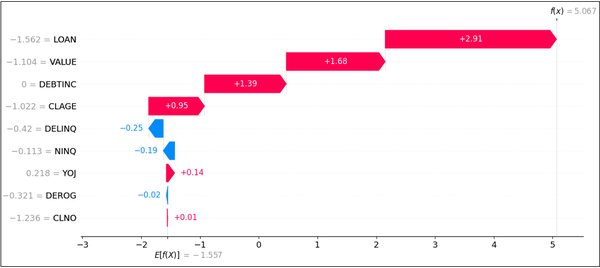
Abbildung 12: SHAP-Wasserfalldiagramm, XGBoost-Modell
Beobachtungen aus den SHAP-Wasserfalldiagrammen
Logit‑Modell: Die Wirkung der Merkmale ist – wie zu erwarten war – proportional und stabil bei der Richtung der Vorzeichen der Regressionskoeffizienten.
XGBoost-Modell: SHAP zeigt teils gegenläufige Effekte gegenüber dem Logit‑Modell (z. B. bei VALUE oder CLAGE), was auf eine unterschiedliche Modellregularisierung hindeutet.
5.3 Nicht lineare Strukturen in SHAP-Scatterplots
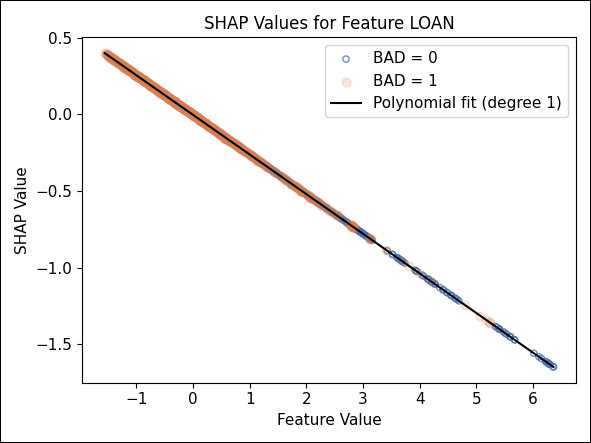
Besonders deutlich wird die höhere Modellkomplexität von XGBoost in den SHAP‑Scatterplots einzelner Merkmale:
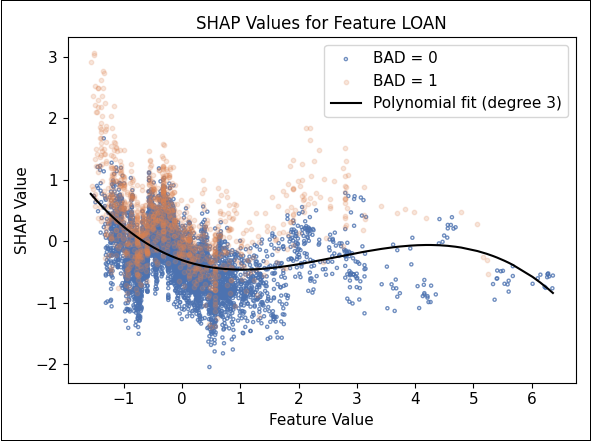
Abbildung 13: SHAP-Werte zum Merkmal LOAN
Beim Merkmal LOAN zeigt das Logit‑Modell eine erwartungsgemäß lineare SHAP‑Beziehung – in diesem Fall heißt das, niedrige beantragte Kreditsummen führen zu einem höheren Risiko (bzw. negativen Beitrag zum Score).
XGBoost hingegen zeigt eine mehrwertige Relation, bei der identische Kreditsummen zu unterschiedlichen SHAP‑Werten führen – ein möglicher Hinweis auf interaktive Effekte mit anderen Merkmalen.
Diese Muster sind nicht über einfache Korrelationen erklärbar – die SHAP-Werte liefern somit genuine Einsichten in die Entscheidungslogik des Modells, jenseits einfacher Regressionsbeziehungen.
5.4 Vergleich der Richtungen der Modelleffekte
In dieser Analyse visualisieren wir die SHAP‑Werte des Logit‑Modells für ausgewählte Merkmale und färben sie entsprechend der SHAP‑Werte des XGBoost-Modells. Es gilt:
Rot: Hohe SHAP‑Werte im XGBoost‑Modell.
Blau: Niedrige SHAP‑Werte im XGBoost‑Modell.
Der Fokus liegt auf den Ausfalldatensätzen des ersten Folds der Kreuzvalidierung aus dem oberen linken Quadranten des Streudiagramms in Abbildung 7, wo das Logit‑Modell die Ausfälle im Gegensatz zum XGBoost‑Modell unterschätzt.
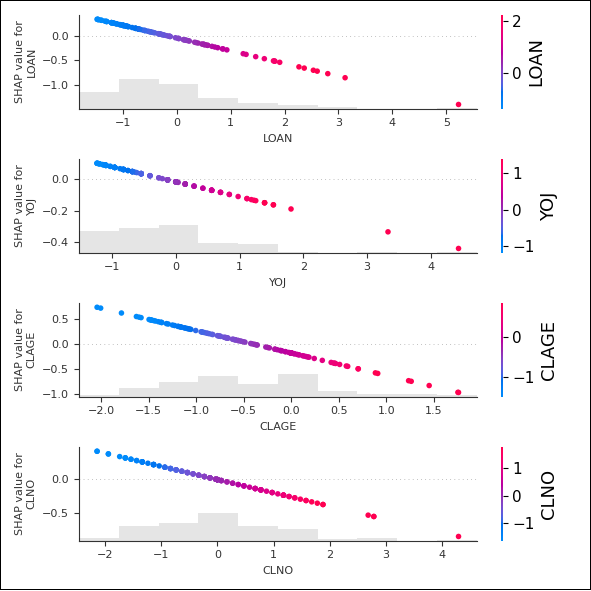
Abbildung 14 zeigt deutlich, dass die Modelle bei den Merkmalen LOAN, YOJ, CLAGE und CLNO entgegengesetzte SHAP‑Werte aufweisen.
Abbildung 14: Vergleich der gegenläufigen SHAP-Werte für ausgefallene Kredite aus Fold 1 im oberen linken Quadranten in Abbildung 7
Während das Logit‑Modell bei steigenden Merkmalswerten einen negativen Verlauf der SHAP‑Werte zeigt, weist das XGBoost‑Modell einen positiven auf. Die Unterschiede deuten darauf hin, dass die Modelle die Bedeutung dieser Merkmale unterschiedlich interpretieren, was zu divergierenden Vorhersagen führt. Ein tieferes Verständnis dieser Abweichungen kann dazu beitragen, die jeweiligen Modellannahmen zu hinterfragen und die Prognosegenauigkeit zu verbessern.
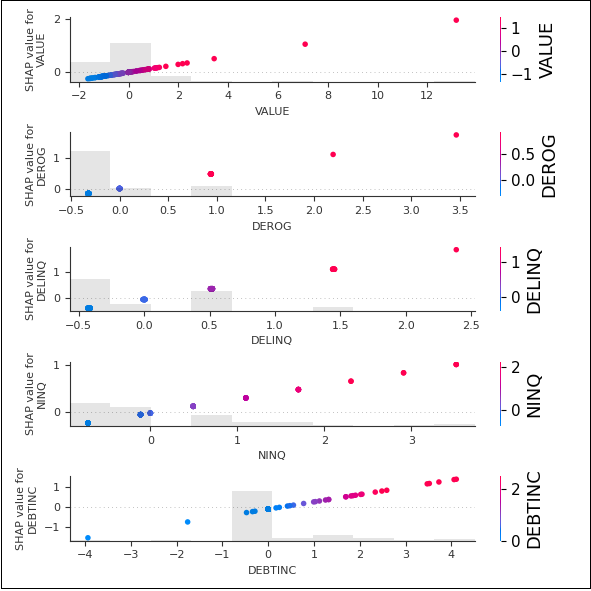
Im Gegensatz dazu zeigt Abbildung 15, dass die Modelle bei den Merkmalen VALUE, DEROG, DELINQ, NINQ und DEBTINC gleichlaufende SHAP-Werteeffekte aufweisen.
Abbildung 15: Vergleich der gleichlaufenden SHAP-Werte für ausgefallene Kredite aus Fold 1 im oberen linken Quadranten in Abbildung 7
Dort, wo das Logit‑Modell bei steigenden Merkmalswerten einen positiven Verlauf der SHAP-Werte zeigt, weist auch das XGBoost‑Modell einen positiven auf.
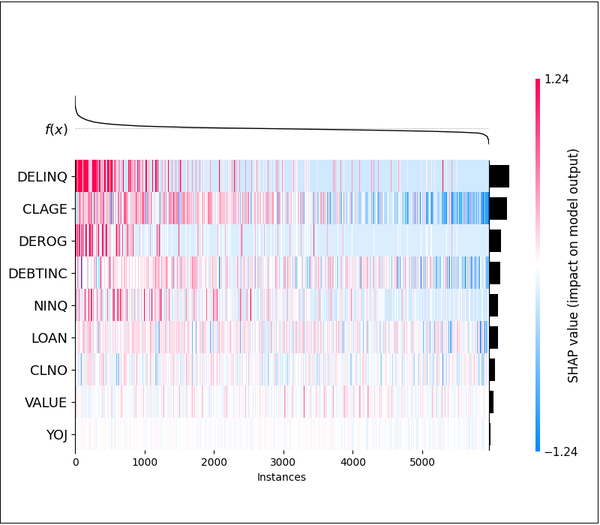
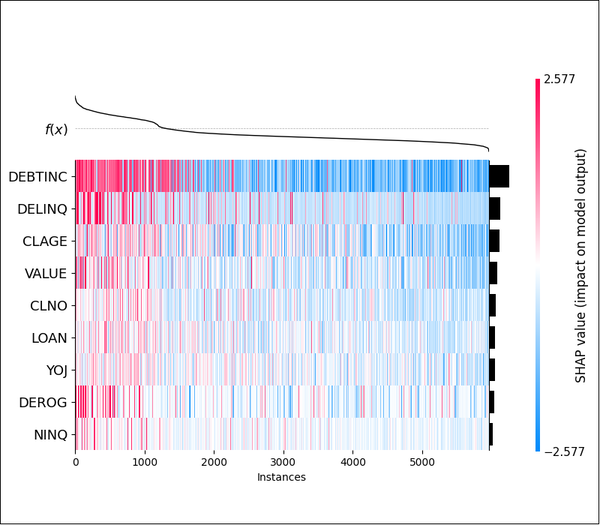
Abbildung 16: SHAP-Heatmaps

Über den Autor
Dr. Andree Heseler ist Geschäftsführer der mex consulting GmbH & Co. KG und Experte für datengetriebene Risikomodellierung.
Er berät Banken und Asset-Manager zu mathematisch fundierten Verfahren des Risikomanagements mit besonderem Fokus auf Modellierung, Validierung und die Anwendung von künstlicher Intelligenz. Seine Erfahrung verbindet Finanzmathematik, Data Science und die Entwicklung modellgetriebener Prototypen in anspruchsvollen Kundenprojekten.